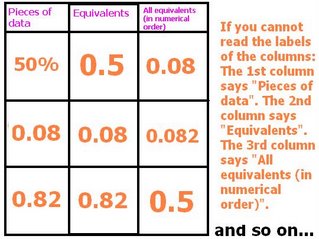
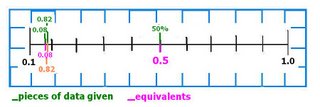
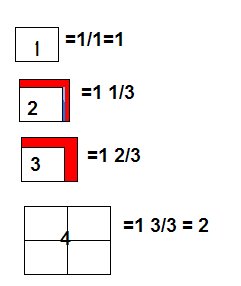
These couple of days in math we have been learning about
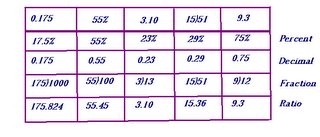
Perfect Squares. A perfect square has whole number factors,( no decimals ) the factors are the same and it has equal sides.
 Why is this a square perfect?
Why is this a square perfect? This square is perfect because there are 3 going across and 3 going down. So this square is a 3x3 square. There is an easier way to write this though. Another way is 3 to the power of 2, or 3 squared, or 3 with a small 2.
Numbers like 1, 4, 9, 16, ect. Can be made into perfect squares. These numbers have something in common. They have whole
square root numbers.
What is a square root? The square root is a number multiplied by itself giving you the square root of a number. For example: The square root of 25 is 5 because when you mulitiply 5 by 5 it gives you 25.
Try it on your calculator. The symbol should look like a division sign( usually you have to use second function) then punch in the S.R. sign then the number 9. What does it give you? the number should be 3 because 3x3=9. So the square root of 9 is 3.
What if the number can't be made into a perfect square? Mostly all numbers can be made into a perfect square. For example if i want to make a square out of 6. This is what you probably would get.
 Is this a perfect square?
Is this a perfect square? Ask yourself these questions. Does it have equal sides? Does it have the same factors? Well, you can turn this rectangle into a perfect square. First try to make the largest perfect square you can make, it's ok if you have remaining
squares. This is what you should have.

Now, you have a perfect square. But what do you do with the remaining 2 squares. You must now think of the 2 squares as just pieces that you can put around the square. Like this:

Now, imagine you take one half of the 2 saquares and put it horizontally on top the the square and the other half next to the square vertically.
What do you get? You should get something that would look like this

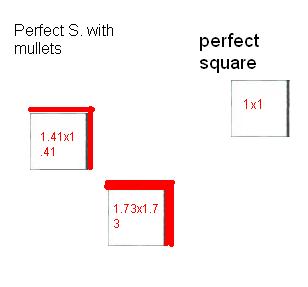
The squares that you add become the
Mullet of the square. The mullet is the remaing squares. Instead of having whole factors they become whole factors with decimals. The mullet is added to squares that do not have whole factor numbers. You can think of the mullet as hair. The more remaining squares you have the longer or bigger the hair(mullet) gets. The less remainders you have the smaller the hair(mullet) is. So the measurments of a perfect square with an area of 6 is 2.44x2.44 or 2.44 to the power of 2.
Mr. Harbeck gave us a test on probability and mean, median and mode, so if you weren't here on that day you will probably take it the next time we have class.
AssignmentsHe also assigned an assignment dealing withe perefect squares. We were given 2 sheets of graph paper and 1 long white peice of paper. You where so post to make perefect squares from 1-16. Four of the squares would have no mullet(1,4,9,16) the rest would have a mullets. If you weren't sure how to paste them onto the paper you could save the squares(ready to paste) and wait till next class.
I'll show you how to get started. This is what the first part should look like this
 you have to write the factors, the exponent and and what the area of the square is.Assignments that are due.
you have to write the factors, the exponent and and what the area of the square is.Assignments that are due.Perfect sqaure chart-three columns(factors, exponent, area) e.g. 25x25, 25 to the power of 2, 625 unit squared.
Journal #1- Which of the numbers are perfect squares? 6,8,9,10, Justify your answers. Prove using pictures, words and numbers.
Journal #2-Make perfect squares out of 6,8,9,10,12,14,17.
Perfect square-long paper withe squares from 1-16*see assignments*
Jaymie S=)
Now, for the next scribe..........
Amy L=)