Blog Etiquette

Hello everyone. I am very pleased to see everyone reading each others scribe posts. I would just like to give you a reminder. We have an international audience that reads these posts and uses them in classes all around the world. Since we have started these blogs many page hits have happened.

I will show you just how many countries are showing up,

Wow. This is why I would like to mention a few points. I love your enthusiasm. I want it to continue. Please for some of the comments you leave use the chat boxes provided to you. comments on peoples blogs must be polite and have no hidden meanings. You are excellent commenters on other peoples scribe posts. I think you do this better then any group I have ever worked with. Please do not stop commenting. Just think before you comment!

I encourage you to strive for excellence and have fun with your blog. It is a legacy that will remain here forever. Please use this tool wisely.

Now with that over I would like to say that the quality of the scribe lately has be beyond my expectations. You are to be congratulated on your terrific work and effort. Keep it going.

Please make note that your first Growing Posts will take place in December. I will keep you informed.

Once again. Remember you have an audience. This blog is an extension of the classroom. Stay in control.

Thank You

Mr. Harbeck

Maxine's Scribe Post: Equivalents

So today in class we corrected our homework. We had to convert numbers into fractions, decimals, percents or ratios. For example 35.5%

Fraction - 355/1000 (hint: If you have a decimal number and you want to get into a fraction you take away the decimal and add a 0 to the denominator)

Decimal - 0.355

Ratio - 355:645

Next you have to place it onto a number line. You have the raw numbers on the top and the equivalent you choose on the bottom. Remember to put the markers because you will have to use them on the test. (0, 25, 50, 75, 100)

If you have any questions about this or need help just ask me and I'd be happy to help.

After we went over that Mr. Harbeck put up an Equivalents Pre-test. You had to fill out a chart and using NO CALCULATOR.

Convert the following values so that you can place them on the number line below. Show all your work.

Try to convert some of your own like 3:2 into a fraction. Or the ones that you find hardest even if you don't want to it'll be for the best!

Try 5/10 into a percent, 0.66 into a ratio, and 46:98 into a decimal.

After you have filled out this chart you have to place the numbers on a number line. *Remember that the raw numbers go on the top and which ever equivalent you choose goes on the bottom, put your markers before you put your numbers*

If you do not get this once again you can always ask me anything. I'm serious!

There was also one more question.
6, 6, 8, 14, 14

How could you determine whether the average of these numbers is greater than 10 without acually computing the average? Explain how you you decided if the average was more than 10 or less than 10.

BTW - You should have your big paper done because it can come in useful. And the unit book is gonna be due on Friday, I think. So have everything ready! And go over the mean, median, mode and range just in case :)

Some websites that can help you study are:

Conversions and Equivalents

Word problems using Equivalents

Ratios

Well that sums it up and I'm gonna choose Boeun to be the next scribe.

Math Pretest Equivalents

Math Pretest

Convert the following values so that you can place them on the number line below. Show all your work.

0.175

55%

3:10

15/51

9:3

How could you determine whether the average of these numbers is greater than 10 or less than 10 without actually computing the average. Explain how you decided the average was more than or less than 10.

Marielle's scribe post: equivalents

During our second period of math (6th period) we first worked on our equivalents numberline (assignment #2) on the long graph paper Mr.Harbeck had given us.


Your finished assignment should look similar to this :





After being given almost half the class to finish the numberline, we were given another assignment titled "Equivalents Assignment 3". It consisted of 4 questions about percent, decimal, ratio, and fraction. You had to convert each one to each of the 4 listed (fraction, decimal,ratio, percent). At the bottom of the questions were the 'personal reflection' which also had to be answered too. If you did not copy down all the questions in class, assignment #3 can be found at the link below:
http://sargentparkmathzone.blogspot.com/2006/11/equivalents-assignment-3.html


If you have forgotten how to convert fractions to decimals or any others, just check your big paper, or janna's scribe (located under Cj's). You may also use these sites I've found:
http://sjh.hsd.ca/deruyck/images/junereview.htm
^^ this site talks about everything we have learned so far in math class. It also contains other things related to math like how to solve word problems, dividing/multiply fractions, and many more.

http://www.sparknotes.com/testprep/books/sat/chapter10section6.rhtml
http://content.class.com/c3_content/lor/mathematics/alg_percents/html/0302_0201.htm



This all pretty much ended our day. Tomorrow there will be a "pre-test" about ratios, fractions,percents, and decimals. The next scribe will be maaxineriLaaay :) [Maxine A]


`Marielle D. 8-17

Cj's Scribe Post: Equivalents

Today, during our first math class, Mr. Harbeck showed us these pieces of data:







With these pieces of data, we were to construct a number line arranging these pieces of data in numerical order:






First, we were to complete a table that showed: the decimal, percent, ratio, or fraction, (that was equivalent to all of the pieces of data); the pieces of data; and all of the equivalents in numerical order:









Then we were to start a rough copy of what we were going to put on the long sheet of graph paper, Mr. Harbeck would be handing out:







On this long sheet of graph paper, we would put what we placed on our table; but the pieces of data would either above or below the number line; showing us what equivalent it matches up with. The equivalents would then be placed above or below, (depending on where you put your pieces of data), and it would, too, match up with its equivalent. However, the numbers would not just be placed ANYWHERE on the number line, but it would be arranged from SMALLEST to LARGEST. In this case below, the pieces of data and equivalents are arranged from 0.1-1.0:









THE NEXT SCRIBE POSTER IS DOCTOR, (MARIELLE D the MD).

!!!Janna's Scribe Post!!!

Well, since Aaron didn't complete or try to do his scribe I get to do the honours of replacing him. To start off class we looked at our homework as quick as we could since we didn't get math the next day(which was Wednesday). Our homework was to find the formula of getting the following below:

Ratio:
to Fraction: The first number or part of the ratio will be the numerator of the fraction. Add the numerator and the denominator to get the second number in the fraction. Part to part.

Example: Ratio is 3:1. Numerator is 3 since 3 is the first number. 3+1=4. 4 is the denominator.

to Decimal: Get a fraction from the Ratio by using the formula above. Then divide the numerator by the denominator to get the decimal.

Example: Ratio is 4:2. Fraction is 4/6. 4 divided by 6 = 0.666666666667

to Percent: First get a fraction form the Ratio. Take the Numerator and divide it by the Denominator to get a decimal. Multiply the decimal by 100.

Example: Ratio is 2:5. Fraction is 2/7. 2 divided by 7= 0.285714 (repeated) x 100= 28.5714285714

Fraction:
to Decimal: Divide the numerator by the Denominator

Example: Fraction is 3/5. 3 divided by 5 = 0.6

to Percent: Divide the Numerator by the Denominator. Take the decimal and multiply it by 100.

Example: Fraction is 1/3. 1 divided by 3 = 0.333333(repeated) x 100= 33.333333(reapeated)

to Ratio: Take the Numerator and make it the first number in the ratio. Then add the numerator and the denominator to get the second number in the ratio.

Example: Fraction is 4/1. 4 is your first number or part. 4+1=5. 5 is your second number or part.

Decimal:
to Fraction: Say the number --> Write the number.

Example: Decimal is 0.48. Say it. 48 hundredths. write it, 48/100.

to Ratio: Turn the decimal to a fraction first. Then take the numerator and make it the first number in the ratio. Take the denominator and subtract the numerator from it to get
the second number in the ratio.

Example: Fraction is 3/8. 3 is the numerator so its the first number or part. 8-3=5. 5 is the second number or part. Ratio is 3:5

to Percent: Take the decimal and multiply it by 100. Simplify if you can.

Example: Decimal is o.83. 0.83 x 100= 83 83/100

Percent:
to Ratio: Take the percentage and get rid of the percent sign. That will be the first number or part. Then subtract the percentage by the value of the bottom number(usually 100) to give you the second number or part.
First number in ratio = the percent
Second number in ratio = (value of number e.g. 100) 100 - percentage

Example: Percent is 46%. 46

to Decimal: Take away the percent signs and divided by 100.

Example: Percent is 37%. 37 divided by 100=0.37

to Fraction: Since percents are out of 100, just take the percent put it over 100 and take away the percent signs. Then Simplify.

Example: Percent is 77%.

HOMEWORK:
Complete the following for our portfolio's':
1. Equivalent Chart
2. Big Paper
3. Quiz 1
4. Equivalent Assignment
5. Quiz 2

Our homework was to finish off boxes four and five on our big papers. It would be ___ to ___ in box 4. Then in box five the formula. (box 3 should be full of pictures).

Also the Equivalent worksheet found below my post, should be completed. The one where you have to find 4 decimals using 1-2-3-4-5-6-7-8-9 and then use your formulas to get the fraction, ratio and percent for them all.

Some websites you can visit are found below:
http://www.mathgoodies.com/lessons/vol4/meaning_percent.html

This site gives you different questions for fractions, ratios, decimals and percents, such as finding fractions from coloured grids. Then compare it to other fractions, ratios, decimals and percents. It also gives you the answer when you click on the word "answer". It includes questions and some ways of solving these problems.

http://www.aaaknow.com/pct.htm
This site shows you formulas to get certain thins from something. Such as a fraction to a ratio ...etc. It is not as useful as the first site above, but it does help if you get stuck on the homework and work shown above in my scribe.

The Next Scribe Is Carmie-Jane (C.J.)

Equivalents the Assignment

Equivalents The Assignment

1. Make 4 different fractions using the digits below. You may only use each digit once. Convert these 4 fractions into decimals, percents and ratios.

1, 2, 3, 4, 5, 6, 7, 8, 9

2. Make 4 different decimal using the digits below. You may only use each digit once. Convert these 4 decimals into fractions, percents and ratios. (Do not use the decimals from the question above).

1, 2, 3, 4, 5, 6, 7, 8, 9

3. Make 4 different percents using the digits below. You may only use each digit once. Convert these 4 percents into fractions, decimals and ratios. (Do not use the fractions and decimals from the questions above).

1, 2, 3, 4, 5, 6, 7, 8, 9

4. Make 4 different ratios using the digits below. You may only use each digit once. Convert these 4 ratios into fractions, decimals and percents. (Do not use the fractions and decimals or percents from the questions above).

1, 2, 3, 4, 5, 6, 7, 8, 9

Fiel's Scribe

Hoy people listen up I'm the scribe for today and I would like to tell you my scribe. So please read it carefully.



Today we start a big paper and in the morning we did a Quiz about fraction, decimal, percentage and ratio.

Mr. Harbeck tell us to found the definition for fraction, decimal, percentage.

And then Mr. Henly shows us one example of ration.

Ration's:

you have 7 candy bars. 3 of them are kit Kat's and 4 of them are mars.

3/7 # 3 is kit Kat's and # 7 is candy bars

4/7 # 4 is mars and # 7 is candy bars

3+4=7

5- Part and 8 - whole

5 and 3 are Part and Part means whole

and that's the example of ratio.


In the after noon, we work on group of four or three and share our definition, and also we did are second Quiz. Its about ratio because many of us didn't understand ratio.



well this is my scribe for today......
thank you for reading it and the next
scribe isssss uhmmm aaron
yeeeessss I'm dooonee

Rommel's scribe post

The first thing that we did in class was to put the square root unit in order which was... the pink paper, the perfect square chart, the fist journal(which ones the perfect square),journal 2 where you had to draw things,the perfect squre the long paper, estimating square roots using chart and biulding problem, estimating square roots using fractions,recipe quiz 1 corrected,quiz 2 corrected, and the test corrected.

Then we got split in groups and got this paper and cards with pictures of decimals, percent, fractions, and pictures.


Ratio tells how one number is related to another number is related to another. A ratio may be written as " A:B " or the phrase " A to B" . A ratio of 1:5 says that the second number is 5 times as large as the first. The following steps will allow determination of a number when one number and the ratio between the numbers is given.

EXAMPLE :
Determine the value of the B if A:B and hte ratio of A:B = 25

-determine how many times the valiable A is divisible by the corresponding portion of the ratio. (6/2=3
-multiply this number by the portion of the ratio prestenting B(3x5=15)
-Therefore if the ratio of A:B is 2:5 and A=6 then B+15

Next scribe is Fiel

Way to Scribe

"Fêtes de Genève"
Originally uploaded by paprikaOptic.

Way to go Room 17. You did seven scribes for seven classes. That is perfect. You are the only class to do this. Keep it up during the Percent Unit. It starts tomorrow. Check the scribe list to see who the scribe can be!!


Remember a good scribe has images, words and links to helpful places to understand the lesson you are scribing.
Mr. Harbeck

kristian's scribe

today we had a test which contains mean, median, and mode,probability,and square root.


this are some of the example that we have on the test:
square root

√22 = 25 - 16= 9 6 /9
22 - 16= 6

√34 = 36 - 25= 11 3/11
34 - 25= 9


mean, median, mode

24 38 36 78 53


24
38
36
78
+ 53
229


probability

red 8 (gray,yellow)
black 4
gray 3 10/22 10÷22=0.454 x 100= 45.4%
yellow 7

well this is my scribe for today.......
thank you for reading it and the next
scribe is Romel

John's Scribe

today we had a test in math and after the test Mr.Hanley teach us a new technique on how to find the denominator of a square root and then Mr.Hanley give us a example.

1-4= /3 so you subtract the smaller perfect square to the larger perfect square.
4-9= /5
9-16= /7

81 182........100
100-81= /19

And then after that he asked us what are the steps for doing this, and then Jannah answered:
1. Find the perfect squares on either side of the square root you are trying to solve.

2. Subtract the smaller perfect square from the larger perfect square.

3. Answer is your denominator.

Mr.Hanley give us this questions to answer:

Estimate each Square Root using FRACTIONS.
/67 /45 /15 /39 /57 /23

/31 /79 /8 /99 /86 /739

/666 /578 /433 /176 /333 /260

A farm has 7 equal square fields with a total area of 616 acres 2. Estimate the dimensions of each field using fractions.


In the afternoon Mr.Hanley give us back our quiz #1 and we have to do the corrections. After we did our corrections, we did our quiz #2 at the back of our paper, and when we finish our quiz he asked us if we have any questions on what were doing and nobody answered. And Mr.Hanley give us a word problems for homework.

Square Root Word Problems
a. Surinam, in South America, is roughly shaped like a square. It covers an area of about 100 489 km2. Find the length of each side of Surinam.

b. A warehouse has an area of 5808 m2. It is divided into 12 equal square sections. Find the dimensions of each section.

c.Estimate the following square roots using fractions:
/78 /189 /90 /34 /125

/145 /66 /218 /756 /867

/493 /555 /389 /678 /299

well that's my scribe post for today thank you for reading it
and the is.........Rommel.

TODAYS SCRIBE BY IAN ABAD

Ladies and gentlemen I would like to tell you my scribe.So please read it carefully.

today, we study how do to estimate the square to a fraction.And this is it start.

When we start the class MR. HANLEY the tallest guy in the room asked as to solve the square root of 110.

so I solve it like this:

/100 /110 /121

100 and 121 are the perfect square between 110.

the factors of 100 is 10 so the square root of 110 is 10.?.

When we finish solving it, MR. HANLEY asked us if do we had any ideas to estimate the square root.

when Jamie told him other idea,he told us the main topic of the subject today, HOW TO ESTIMATE THE SQUARE TO FRACTION.

and he asked to solve these:

and i solve it like this:

and then he asked as to solved the square root of 19 by fraction

and this is how i solve it:

/16 /19 /25

I look for perfect square between 19.And I found 16 and 25.I did it by looking for perfect square chart.Then I look for 19 and 19 is the 3rd square after 16 so the numerator is 3 then i look for denominator by counting 17 to 25 and the denominator is 9.the last i had to find the whole number by looking to the perfect square chart and i found that 16 is the 4Th perfect so 4 is the whole number.

so the answer is 4 3/9.

and this is our homework today:

find the square root by fraction.

/9

/10

/11

/12

/13

/14

/15

/16

thank you for reading the royal scribe of Ian. :p

and the next scribe is Kristian

ha ha ha I'm done.

there are some mistake in my first one so I correct it.

November 7 scribe notes by Jorel

today we learned the perfect square. we looked at our perfect square chart, and answer this questions:
find the square roots of these number and is it perfect or not:

1) 25 = 5x5 perfect square
2) 89 = 9.?x9.? not perfect square
3) 64 = 8x8 perfect square
4) 225 = 15x15 perfect square
5) 169 = 13x13 perfect square
6) 784 = 28x28 perfect square
7) 625 = 25x25 perfect square
8) 49 = 7x7 perfect square
9) 594 = 24.?x24.? not perfect square
10) 121 = 11x11 perfect square
11) 765 = 27.?x27.? not perfect square
12) 429 = 20.?20.? not perfect square
13) 654 = 25.?x25.? not perfect square
14) 6 = 2.?x2.? not perfect square
15) 333 = 18.?x18.? not perfect square
16) 852 = 29.?x29.? not perfect square
17) 199 = 14.?x14.? not perfect square
18) 841 = 29x29 perfect square

A warehouse has an area of 2940 meter square. It is divided into 15 equal sections. Find the dimensions of each section.

2940x2940 = 8 643 600

8 643 600 / 15 = 576 240

Each section has 576 240. The square root of 576 240 is 759.1 so its not perfect square

Perfect does not have decimals

tomorrow's scribe isssssssssssssss Ian

Kyle's long overdue Scribe Post!!

kk mr.harbeck dont get mad at me for not really knowing how to post something so im gonna put my scribe here.

The first part of class we pulled out our homework from yesterday. After we used these tiles to try to make a square out of 10 tiles.
But no one can do it until Mr.Hanly showed us how. He showed us that if it is 4x4 so that would make it a perfect square but if we had to do 3x3, We wouldnt be able to make it perfect, so we give it a mullet. Like if it didnt have enough to make it perfect, it would get a mullet.
For Example:

1.1x1
2.2?x2?
3.3?x3?
4.4x4
5.5?x5?
6.6?x6?
7.7?x7?
8.8?x8?
9.9x9
10.10?x10?

New Numbers for homework.
12,14,17

Make squares out of all the numbers

Next scribe is Jorel.

hi Mr.H i signed on to the blog

Hello people I'm your scribe for today. This is for the people who were gone for the last period of the day (math) or sleeping during class...


What we did:
4 x3 = 12
factors product

What shape do u make when multiply?
-rectangle
all rectangles with 10 squares.
==============================
10
Factors = product
1x10=10
2x5=10
==============================
16
fxp
1x16=16
2x8=16
4x4=16
==============================
36
fxp
1x36=36
2x18=36
3x12=36
4x9=36
6x6=36
==============================
4x4=16 or
the fast way would be: 4 whith a litle small 2
beside the 4 ...
4squared2



***important***
A perfect square whose side leghts are ''whole numbers''


*****Homework*****

make a chart:
fraction exponent area
x1 1square2 1unit2
2x2 2square2 4unit2
3x3 3square3 9unit2

make the continuous lines of the chart to "30x30"


****do not pay attention to this scribe***** it is a re-copy



alex m

November 3rds Scribe Notes

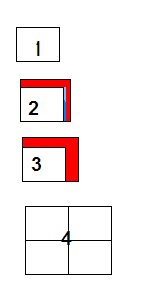
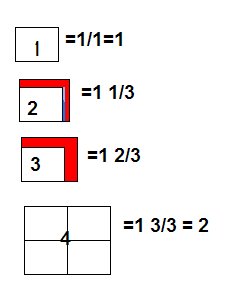
These couple of days in math we have been learning about Perfect Squares. A perfect square has whole number factors,( no decimals ) the factors are the same and it has equal sides.



Why is this a square perfect? This square is perfect because there are 3 going across and 3 going down. So this square is a 3x3 square. There is an easier way to write this though. Another way is 3 to the power of 2, or 3 squared, or 3 with a small 2.


Numbers like 1, 4, 9, 16, ect. Can be made into perfect squares. These numbers have something in common. They have whole square root numbers.

What is a square root? The square root is a number multiplied by itself giving you the square root of a number. For example: The square root of 25 is 5 because when you mulitiply 5 by 5 it gives you 25.

Try it on your calculator. The symbol should look like a division sign( usually you have to use second function) then punch in the S.R. sign then the number 9. What does it give you? the number should be 3 because 3x3=9. So the square root of 9 is 3.

What if the number can't be made into a perfect square? Mostly all numbers can be made into a perfect square. For example if i want to make a square out of 6. This is what you probably would get.



Is this a perfect square? Ask yourself these questions. Does it have equal sides? Does it have the same factors? Well, you can turn this rectangle into a perfect square. First try to make the largest perfect square you can make, it's ok if you have remaining


squares. This is what you should have.




Now, you have a perfect square. But what do you do with the remaining 2 squares. You must now think of the 2 squares as just pieces that you can put around the square. Like this:





Now, imagine you take one half of the 2 saquares and put it horizontally on top the the square and the other half next to the square vertically.






What do you get? You should get something that would look like this

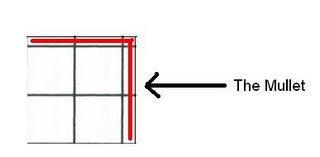
The squares that you add become the Mullet of the square. The mullet is the remaing squares. Instead of having whole factors they become whole factors with decimals. The mullet is added to squares that do not have whole factor numbers. You can think of the mullet as hair. The more remaining squares you have the longer or bigger the hair(mullet) gets. The less remainders you have the smaller the hair(mullet) is. So the measurments of a perfect square with an area of 6 is 2.44x2.44 or 2.44 to the power of 2.

Mr. Harbeck gave us a test on probability and mean, median and mode, so if you weren't here on that day you will probably take it the next time we have class.

Assignments

He also assigned an assignment dealing withe perefect squares. We were given 2 sheets of graph paper and 1 long white peice of paper. You where so post to make perefect squares from 1-16. Four of the squares would have no mullet(1,4,9,16) the rest would have a mullets. If you weren't sure how to paste them onto the paper you could save the squares(ready to paste) and wait till next class.


I'll show you how to get started. This is what the first part should look like this




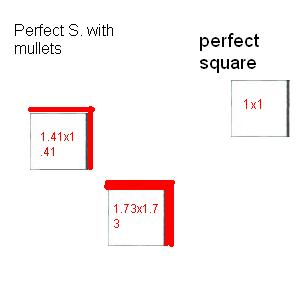you have to write the factors, the exponent and and what the area of the square is.

Assignments that are due.
Perfect sqaure chart-three columns(factors, exponent, area) e.g. 25x25, 25 to the power of 2, 625 unit squared.
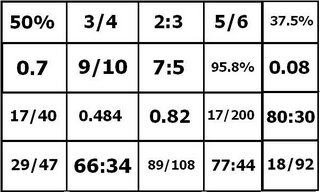
Journal #1- Which of the numbers are perfect squares? 6,8,9,10, Justify your answers. Prove using pictures, words and numbers.
Journal #2-Make perfect squares out of 6,8,9,10,12,14,17.
Perfect square-long paper withe squares from 1-16*see assignments*


Jaymie S=)
Now, for the next scribe..........
Amy L=)

Squareroots and More

Square Roots

This will be a quick unit on Square Roots and Square Numbers. What Are they does this video help?

During this unit the Scribes will be at work. Please choose a person from the Scribe List to be the next scribe. The Scribe list can be found in the sidebar under the category other Sargent Park Math Blogs. Tell that person at school as well as on your scribe post. Please label your post Scribepost.

Happy Scribing


Homework Assignment 1
Which of these numbers can be Perfect Squares. 6,8,9,10. Justify your answers using pictures, words or numbers.

Mr. Harbeck